离心压缩机叶轮S2流面正反命题的研究
作者:劲锋机械发布日期:2018-06-08
离心压缩机叶轮S2流面正反命题的研究
摘要: 分别对流线曲率法正反两类命题进行了研究。正问题中,利用背掠式带分流叶片离心压缩机叶轮算例,计算出子午面流场,对该叶轮进行了性能分析。在反问题中,根据给定设计点参数,设计出了一背掠式叶轮。鉴于气体涡分布的重要性,讨论了不同类型分布对叶轮性能的影响,得出后加载型分布适合离心压缩机叶轮的结论。 关键词: 离心式压缩机 ; 流线曲率法;性能分析;全可控涡;设计 中图分类号: TH452 文献标识码:B 文章编号: 1006-8155(2007)06-0012-06 Research on the Forward and Inverse Proposition of S 2 Surface of Centrifugal Compressor Impeller Abstract: This paper focuses on the forward and inverse proposition of streamline curvature method. In the forward proposition, a back-swept impeller with splitters is employed as a sample, the flow field in meridian surface is calculated, and the performance of this impeller is further analyzed. In the inverse proposition, a back-swept impeller is designed upon the parameters of design point. For the significance of vortex distribution, different types of vortex distribution and corresponding flow fields are presented, and come to the conclusion that the later-loading type gives better performance for centrifugal impeller. Key words: centrifugal compressor; streamline curvature method; performance analysis; all-controlled-vortex; design 1 流线曲率法概述 自吴仲华教授 1952 年发表论文 A General Theory of Three Dimensional Flow in Subsonic or Supersonic Turbomachines of Axial, Radial, and Mixed Flow Types ,提出了两类相对流面理论(简称 S 1 流面和 S 2 流面),把三元流动分解为两个流面上的二元流动问题来求解,为叶轮机械内部流动的计算奠定了扎实的理论基础。 应用两类相对流面理论计算叶轮机械内部流场的方法有多种,其中工程界应用最多,思路最为简洁的是流线曲率法。因其控制方程的系数中包含有流线曲率,故而得名。流线曲率法有两个显著的特点:首先,它将有粘性的流动简化为无粘性的流动;另外,它把一个通过流面约束得到的二维(流函数或势函数)偏微分方程,进一步简化为一维常微分方程,并且未引入任何附加假设。 流线曲率法的求解,一般分为正命题和反命题两类。 正命题就是根据已有的叶轮叶片和轮盘形状,求解出叶轮内部流场。因此,正问题也可以称为性能分析问题。 反问题则反之,即根据规定的速度分布,设计出叶片形状。因此,反问题也可以称为设计问题。 在通流理论模型下,流线曲率法正反两类命题的求解建立在 4 个基本假定的基础上: (1) 控制方程建立在准正交线—流线坐标系下; (2) 流动过程无粘性,但考虑粘性损失引起的熵增,气体的热力过程为多变过程; (3) 流动过程绝热; (4) 在绝对和相对坐标系下,流动分别是绝对定常和相对定常; (5) 平均相对流面为连续光滑的空间曲面。 2 流线曲率法正命题 2.1 控制方程 速度梯度方程 [1] : |
|
|
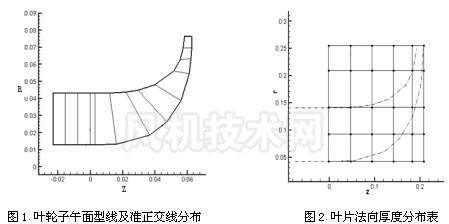 |
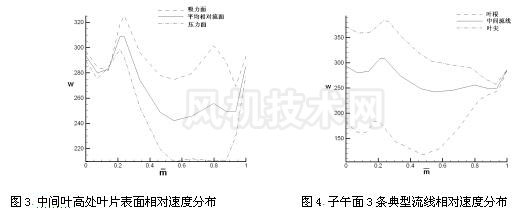
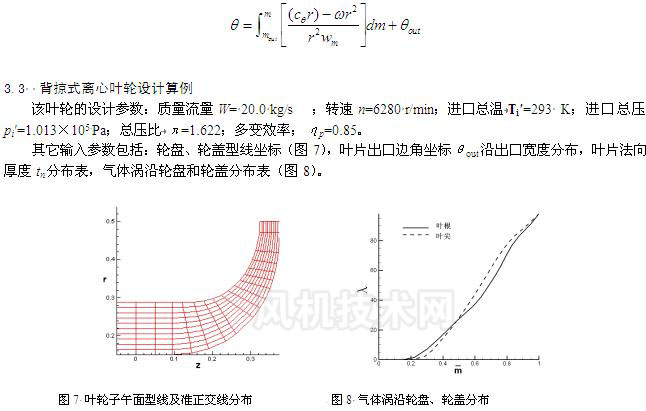
其他的输入参数包括:轮盘、轮盖型线坐标,叶片角坐标 θ 沿轮盘和轮盖的分布,叶片法向厚度 t n 分布表。盘盖型线根据常规一元设计得出,示于图 1 。叶片法向厚度分布表用于计算站厚度差值,示于图 2 。 2.4 计算结果及分析 相对速度在平均相对流面沿叶根、中间流线和叶尖 3 条流线的变化示于图 3 。流线相同位置处,轮盖处相对速度最大,中间流线次之,轮盘处最小。 中间叶高处叶片吸力面、压力面和平均相对流面相对速度沿流线的变化曲线示于图 4 。相同流线位置处,吸力面相对速度值最大,平均相对流面次之,压力面最小,这种分布规律符合实际。因为压力面是工作面,表面压力大;吸力面是非工作面,表面压力小;平均相对流面的压力介于两者之间。根据伯努利方程,压力大则速度小,因而图 4 的相对速度变化规律与理论相符合。 |
 |
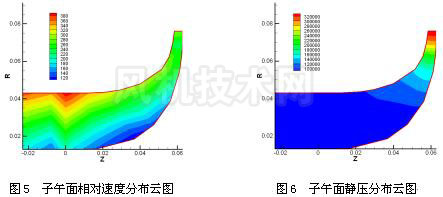
叶轮子午面相对速度分布云图如图 5 所示。通过该图发现,除轮盘转角处的低速区和进口处轮盖附近的高速区外,整个子午流道内相对速度分布比较均匀,尤其是径向流动部分。由此说明该叶轮参数设计较为合理。 叶轮子午面静压分布云图如图 6 所示。通过该图发现,静压沿子午流面逐步升高,其间没有出现压力异常区域。对比进出口静压,转子静压比达 3.2 ,符合设计要求。 综合以上几点分析,该叶轮参数设计获得了很好的相对速度、静压、静温分布,性能基本达标。 |
 |
3 流线曲率法反命题 3.1 反命题的“全可控涡”方法 进行反命题设计的关键是直接提供控制气动性能的手段——设计准则。美国的 Jansen 于 1970 年发表论文提出了设计离心叶轮叶片的“规定载荷法”。该方法通过控制叶轮流道内 1 至 2 根流线的加载规律来设计扭曲叶片,改变了以往利用手工作图或计算机通过几何或纯数学方法构造叶片形状,再利用计算机进行叶轮内流场分析,进而修改叶片形状的设计方法。 西安交通大学的苗永淼、王尚锦于 1974 年提出了利用流线曲率法逆命题公式解决径、混流式三元叶轮扭曲叶片的基本思想,并逐步形成了独特的通过对叶轮内全流场控制来设计叶片的“全可控涡”设计方法,该方法已被试验和工业应用证明了其先进性和可靠性。 “全可控涡”方法的设计准则是给定叶轮内整个子午面上气体涡 ( c θ r ) 的分布来实现控制子午面内整个流场的目的 [3] 。通过求解经过改造的速度分布方程式,直接得出叶片型面坐标和 S 2 流面速度分布。 3.2 控制方程 速度梯度方程: |
 |
 |
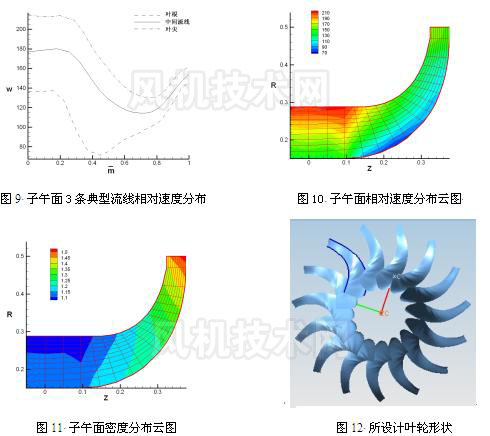
3.4 计算结果及分析 在图 7 所示的环量分布下,相对速度沿轮盘、中间流面、轮盖的分布如图 9 所示。 相对速度在子午面的分布如图 10 所示。从图中发现,在轮盖进口处存在高速区,这是由于轮盖进口处叶轮转速较高;在轮盘转弯处存在低速区,这与实际流动情况吻合较好,因为在靠近轮盘一边,气流是先扩压,容易发生分离,但是转弯后的通道呈收敛型,即使分离发生,也会受到抑制,因此轮盘处低能气流区仅仅局限于转弯处,不再向后传播。 气体密度在子午面内的分布如图 11 所示。从图中看出,在子午面内气体密度沿流线逐步升高,进出口密度比达到 1.5 ,实现了压缩目的。 设计出的叶轮形状如图 12 所示。可以发现在图 8 环量分布下,叶片从进口到出口具有较大的扭曲,这样可以满足指定的加功规律。 |
 |
4 气体涡(环量)分布对相对速度分布的影响 在流线曲率法反问题计算中,沿轮盘和轮盖的气体涡分布是十分重要的输入参数。叶轮机械中,对单位质量气体所做的功为 |
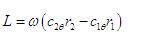 |
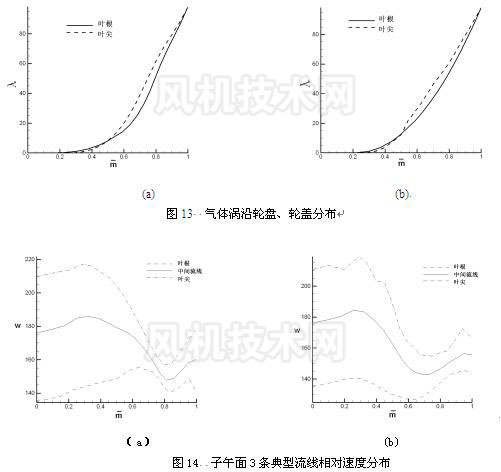
从上式看出,叶轮进出口环量差值决定了加功量的大小。同时,环量沿流线分布规律的不同,所得气流流型也不一样。环量沿流线分布有 3 种类型:前加载型、均匀加载型、后加载型。 图 13 给出了 3 种环量分布;图 14 显示的是相应的沿轮盘、轮盖和中间流线的相对速度分布;图 15 显示了子午面相对速度分布。 |
 |
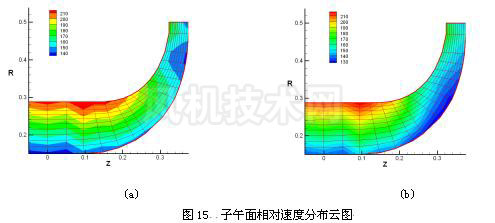 |
比较上面 3 组图形得出结论: (1) 两组气体涡的变化趋势基本一致,为后加载型。这种加载规律符合叶轮内气体流动情况。因为在叶轮通道前部,气流主要沿轴向运动,加功量小;而叶轮通道后部,气流沿径向运动,环量变化剧烈,加功量大。气体涡的其他两种分布类型显然不适合离心叶轮的内部流动; (2) 子午面上,轮盘处往往存在低速区,而轮盖处则存在高速区。气体涡分布不同则这两个速度异常区域会沿流线前后移动或扩大,使得叶轮表现出不同性能。 5 结论 本文对流线曲率这一经典理论的正反两类命题作了深入研究,并对气体涡的分布及其对叶轮相对速度分布的影响作了讨论,得出重要结论: (1) 流线曲率法假设流动无粘性,但粘性修正至关重要,本文引入分离半径 r b 作为判别气流分离与否的标准; (2) 气体涡的分布是叶轮叶片设计的关键,合理的分布能够提高叶轮性能。对于离心式压缩机叶轮宜选择后加载型气体涡分布。 参 考 文 献 [1] 西安交通大学透平压缩机教研室 . 离心式压缩机原理 [M]. 机械工业出版社, 1980.9. [2] Michael R. Vanco, FORTRAN Program for Calculating Velocities in the Meridional Plane of a Turbomachine Ⅰ -Centrifugal Compressor, NASA TN D-7601, 1972. [3] 王尚锦 . 离心压缩机三元流动理论及应用 [M]. 西安交通大学出版社, 1991.6. |
下一条: 离心式压缩机叶轮的分类





